# Slope

## Definition

The slope used in all Cassiopée's modules is the topographic slope:

> The grade (also called slope, incline, gradient, mainfall, pitch or rise) of a physical feature, landform or constructed line refers to the tangent of the angle of that surface to the horizontal. (Source: [Wikipedia](https://en.wikipedia.org/wiki/Grade_(slope)))

![Longitudinal cross-sectional scheme of a rectilinear section](pente.png)

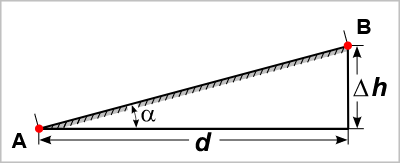
The slope (\(I\)) in m/m used in Cassiopee's modules is:

$$ I = \Delta h / d = \tan(\alpha) $$

<div style="position: relative"><a id="loutil-pente" style="position: absolute; top: -60px;"></a></div>

**Important**:

All calculation modules consider a descending slope as positive except for the "Jet Impact" module where a positive slope will be considered as rising and vice versa. To invert the slope in a calculation sequence of linked modules, use the "linear function" module with \(a= -1\) and \(b=0\).

## The "Slope" module

This tools allows to calculate the missing value of the four quantities:

- upstream elevation (\(Z_1\)) in m;
- downstream elevation (\(Z_2\)) in m;
- length (\(d\)) in m;
- slope (\(I\)) in m/m, with \(I = \frac{(Z_1 - Z_2)}{d}\).